Equations Involving Rational Exponents
Equations involving rational exponents can be solved by combining the methods
that you just learned for eliminating radicals and integral exponents. For
equations involving rational exponents, always eliminate the root first and the
power second.
Example 1
Eliminating the root, then the power
Solve each equation.
a) x2/3 =4
b) (w - 1)-2/5 = 4
Solution
a) Because the exponent 2/3 indicates a cube root, raise each side to the
power 3:
| x2/3 |
= 4 |
Original equation |
| (x2/3)3 |
= 43 |
Cube each side. |
| x2 |
= 64 |
Multiply the exponents:
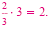 |
| x |
= 8 |
or |
x = -8 |
Even-root property |
All of the equations are equivalent. Check 8 and -8 in the original equation. The
solution set is {-8, 8}.
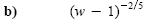 |
= 4 |
Original equation |
| [(w - 1)-2/5]-5 |
= 4-5 |
Raise each side to the power -5 to eliminate
the negative exponent. |
| (w - 1)2 |
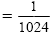 |
Multiply the exponents:
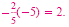 |
| w - 1 |
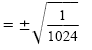 |
Even-root property |
| w - 1 |
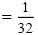 |
or |
w - 1 |
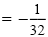 |
| w |
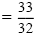 |
or |
w |
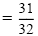 |
Check the values in the original equation.The solution set is
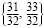 . .
An equation with a rational exponent might not have a real solution because all
even powers of real numbers are nonnegative.
Helpful hint
Note how we eliminate the
root first by raising each side
to an integer power, and then
apply the even-root property
to get two solutions in Example 1(a). A common mistake is
to raise each side to the 3/2 power and get x = 43/2 = 8. If
you do not use the even-root
property you can easily miss
the solution -8.
|